根据系统框图写出系统的方程是信号与系统课程中的一种常见题型。这类题往往能根据框图写出一个含有中间变量的常微分方程组。
问题引入
已知系统框图如下图所示。
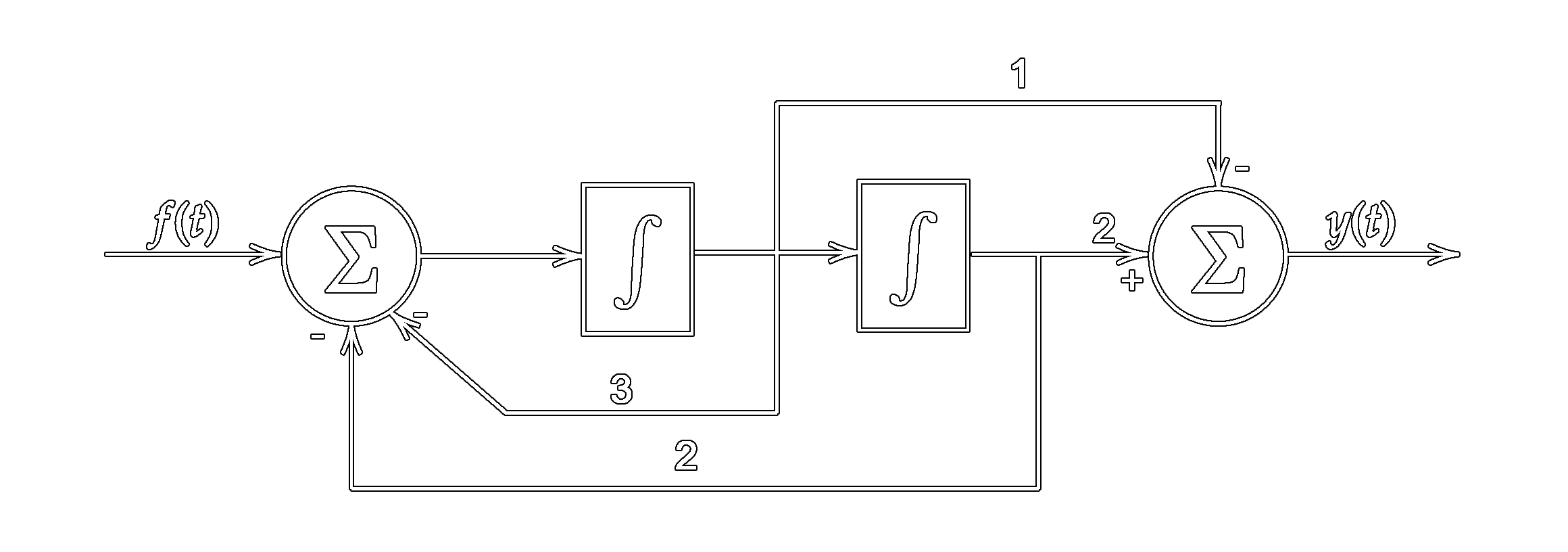
要求写出系统的方程。
问题解析
系统中存在反馈,直接写方程非常不直观,因此设计中间变量,如下图所示。
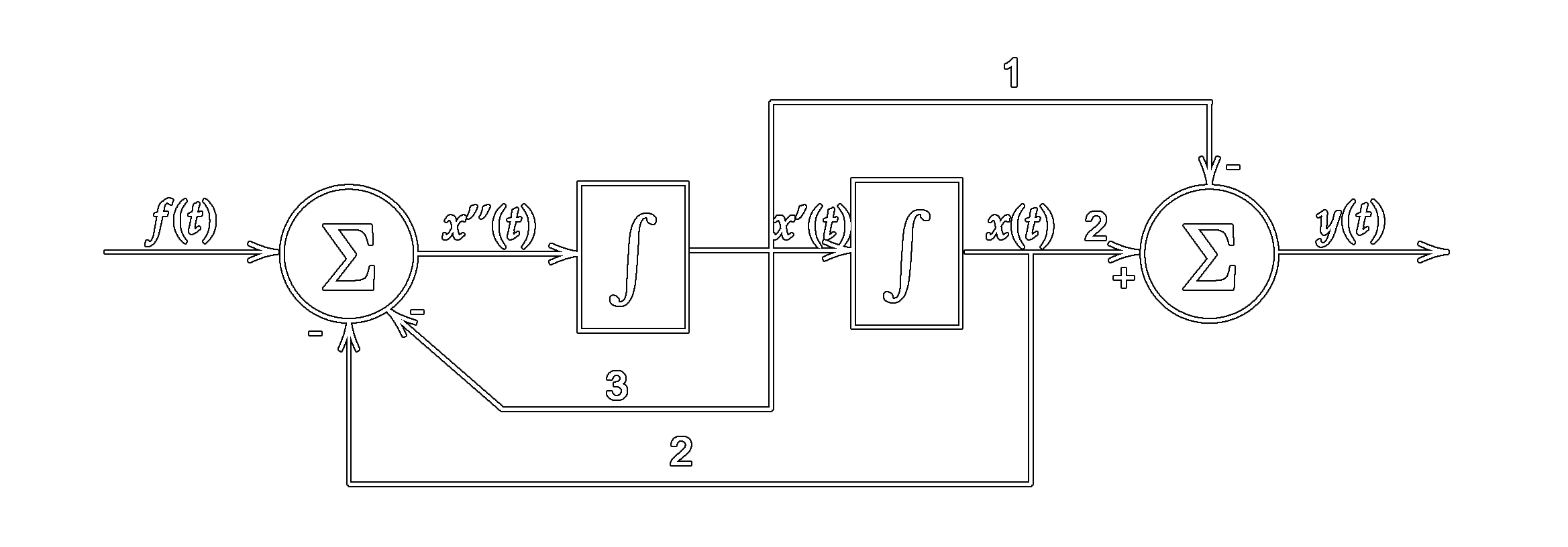
有了这个框图,就能很轻易地写出系统方程。
\[\begin{aligned} f(t) & = x''(t) + 3x'(t) + 2x(t) \\ y(t) & = -x'(t) + 2x(t) \end{aligned}\tag{2.1}\]解方程
下一步就是解这个方程组。
初等变换
本方法由@Mingyue Shao提供
对$(2.1.2)$求导得
\[y'(t)=-x''(t)+2x'(t)\]代入$(2.1.1)$消去$x’‘(t)$得
\[-y'(t)+5x'(t)+2x(t)=f(t)\]上式求导得
\[-y''(t)+5x''(t)+2x'(t)=f'(t)\]利用式$(1)$消去$x’‘(t)$得
\[-y''(t) + 12x'(t)-5y'(t)=f'(t)\]$(2) \times 2 - (4)$得
\[y''(t)+3y'(t)-2x'(t)+4x(t) = -f'(t)+2f(t)\]利用$(2.1.2)$消去$x$得
\[y''(t) + 3y'(t) + 2y(t) = -f'(t) + 2f(t).\]拉普拉斯变换
首先我们定义对于任意信号$f(t)$,其拉普拉斯变换为
\[F(s) = \mathcal{L}\left[ f(t)\right]. \tag{3.1}\]而我们知道拉普拉斯变换的时域微分特性
\[\mathcal{L}\left[ \frac{d}{dt}f(t) \right] = sF(s). \tag{3.2}\]因此对方程组$(2.1)$做拉普拉斯变换可得
\[\begin{aligned} F(s) & = (s^2 + 3s + 2)X(s); \\ Y(s) & = (-s + 2)X(s). \end{aligned} \tag{3.3}\]消除$X(s)$得
\[(s^2 + 3s + 2)Y(s)=(-s + 2)F(s). \tag{3.4}\]拉普拉斯逆变换得
\[y''(t) + 3y'(t) + 2y(t) = -f'(t) + 2f(t). \tag{3.5}\]当然,都有拉普拉斯变换了,不妨更进一步求出单位冲激响应$h(t)$。
由$(3.4)$易得系统函数为
拉普拉斯逆变换得
\[h(t)=\left( 3e^{-t} - 4e^{-2t} \right)u(t). \tag{3.7}\]其中$u(t)$为单位阶跃函数。
魔法
拉普拉斯的求解过程简单明了,但这个题是作为信号与系统课的线性时不变系统章节的例题出现的。
笔者这里给出一个基于线性时不变系统性质的定性分析法,缺乏严格的数学证明,但更能把握线性时不变系统的本质。
线性时不变系统
首先回顾线性时不变系统。所谓线性系统,就是指系统激励的线性叠加所产生的响应也是对应的响应的线性叠加。
系统$Y$在激励$f_1(t)$下的响应为$y_1(t)=Y[f_1(t)]$,在激励$f_2(t)$下的响应为$y_2(t)=Y[f_2(t)]$;
如果$Y[a_1f_1(t) + a_2f_2(t)] = a_1y_1(t) + a_2y_2(t)$则系统为线性系统。
所谓时不变系统,是指系统的激励的延时对应的响应也对应延时。
系统$Y$在激励$f(t)$下的响应为$y(t)=Y[f(t)]$,如果$y(t-t_0) = Y[f(t-t_0)]$则系统是时不变的。
例题
判断线性和时不变性 $ y(t) = \int_{-\infty}^{5t}f(\tau)d\tau $
显然是线性时变的,留给读者自证,欢迎在评论区交流。
回顾完线性时不变系统,我们回头看一下方程$(2.1)$。
\[\begin{aligned} f(t) & = x''(t) + 3x'(t) + 2x(t) \\ y(t) & = -x'(t) + 2x(t) \end{aligned}\tag{2.1}\]如果将$x(t)$看作激励,$f(t)$和$y(t)$看作两个系统$F$和$Y$的响应,不难发现系统$Y$和$F$是线性时不变的。
如果将信号$f(t)$和$y(t)$再作为激励输入到系统$Y$和$F$中,如下图所示。
这时会很自然地认为,最后两个响应应该是相等的,毕竟他们经过的系统是一样的。
\[F\left[ \: Y\left[ \: x(t) \right] \right] = Y\left[ \: F\left[ \: x(t) \right] \right] \tag{3.8}\]就像对两个函数先做加减运算还是先做微分运算一样,加法和求导是可以颠倒顺序的。
\[\left[ \sum_{n=1}^{m}f_n(t) \right]' = \sum_{n=1}^{m}f_n'(t) \tag{3.9}\]这样我们就可以得到
\[\begin{aligned} F\left[ y(t) \right] &= Y\left[ f(t) \right] \\ \Rightarrow y''(t) + 3y'(t) + 2y(t) &= -f'(t) + 2f(t). \end{aligned}\tag{3.10}\]这个自然的看法在本题中是成立的,这一点不难从拉普拉斯变换的推导过程中看出。系统的微分操作最后都变换成了乘法,而乘法确实有结合律和交换律,所以本题可以这样定性分析得出正确的答案。
以笔者目前的实力,并没有方法将这个自然的看法推广到所有线性时不变系统。读者如果有兴趣或者了解相关内容,不妨在评论区留言。

